Procedimiento. Para calcular el área bajo la gráfica de una función f f, se utiliza la definición de la integral definida. donde f f es continua en el intervalo [a,b] [a,b] y F F es una primitiva de f f. En este caso, para encontrar el área entre dos curvas, calculamos primero el área debajo de la mayor y restamos el área de la menor.. Podemos calcular el área de la región limitada por las gráficas de dos funciones y dos rectas verticales. El intervalo se modifica desplazando en la vista gráfica los puntos respectivos. En las casillas de entrada podemos introducir cualquier función continua. Observa la diferencia entre el valor de la integral de la diferencia de las.

Area limitada por tres curvas con geogebra YouTube

Área de la región limitada por 2 curvas Integral Definida + GeoGebra Ejercicio 3 YouTube

Integral Definida Área de Región Limitada entre Curvas Clase Virtual YouTube

29 Ejercicios de área entre dos funciones I YouTube

Área limitada por una función, el eje OX y las rectas x=a y x=b. Vídeo 2 YouTube
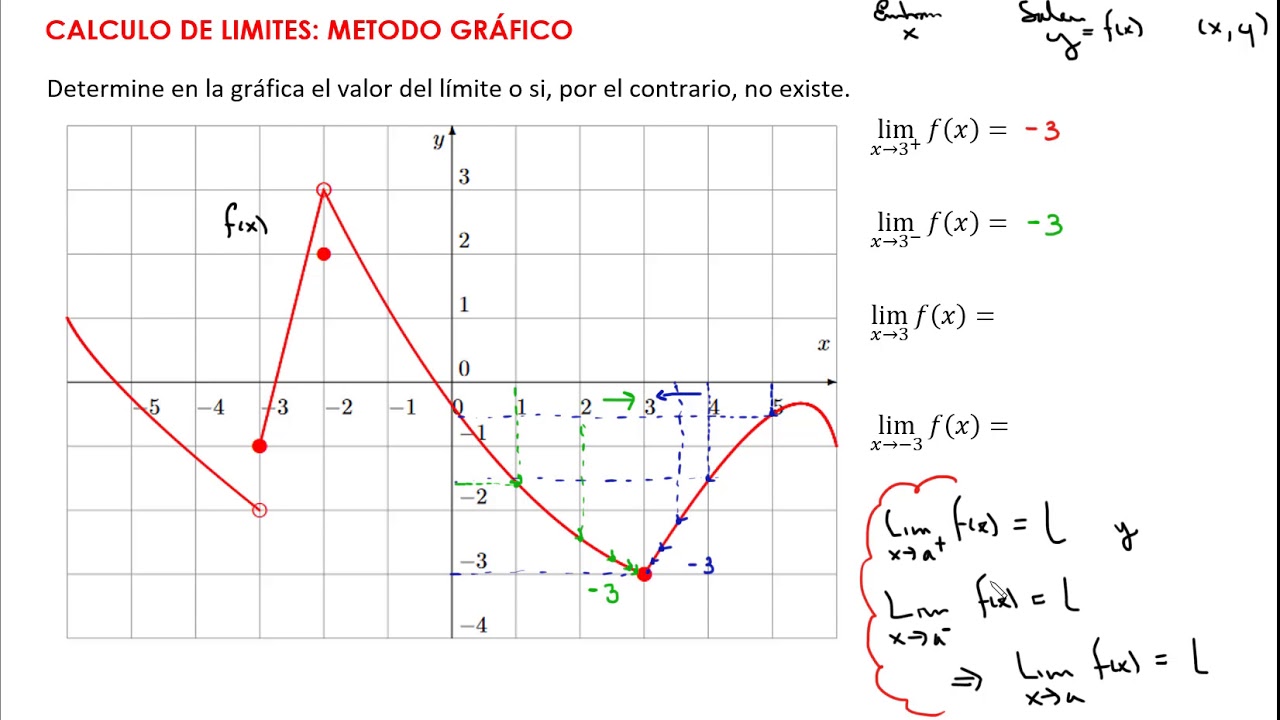
Calculo de limites de una función método gráfico Ej. 1 YouTube

Encuentre el área de la región limitada por las gráficas de f(x)=2Cos(x) y g(x)=x/2 Interprete

Área limitada por las graficas de dos funciones Ejercicio 01 YouTube

Cómo Calcular Determinar el Área entre Dos Funciones Curvas Graficas en un Intervalo 3 YouTube

ÁREA ENTRE DOS CURVAS // APLICACIÓN DE LA INTEGRAL DEFINIDA YouTube

Area de una region limitada por dos curvas con geogebra YouTube

Trazar la región acotada por las gráficas de las funciones y determine el área de la región

Área usando la integral doble de la región acotada por y=4x^2, y=x+2 YouTube

Área Entre Delimitada por Dos Funciones Bajo una Curva función y Recta Cálculo Integral Definida
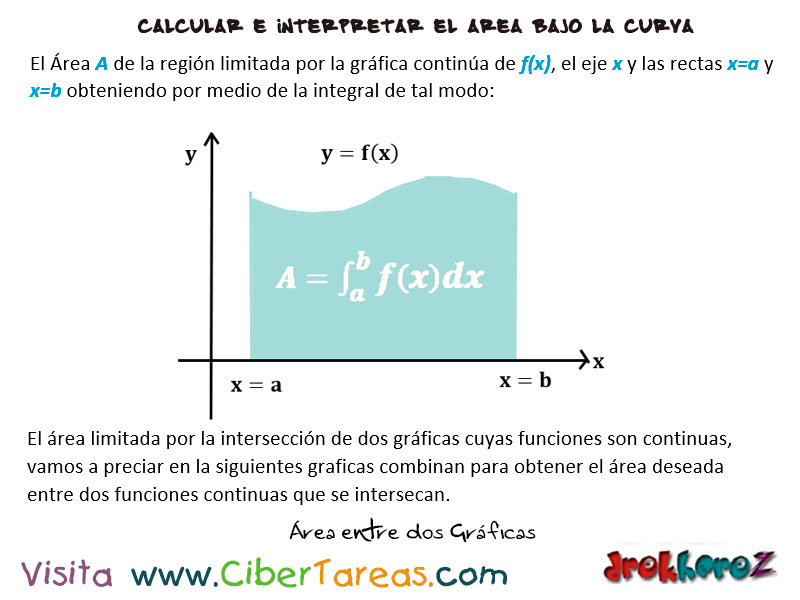
Área entre dos gráficas Cálculo Integral CiberTareas

área limitada por las gráficas seno y coseno EJERCICIO 2 YouTube

Utilice una integral doble para calcular el área de la región limitada por las gráficas de las

Calculo Integral Área de una región limitada por tres curvas. Aplicación de la integral definida.

Área entre la gráfica de funciones YouTube

Cálculo de área limitada por dos funciones YouTube
Tema: Área. Podemos calcular el área de la región limitada por las gráficas de dos funciones secantes en más de un punto. Al cargar puede ser necesario actualizar la construcción para que se calculen adecuadamente los puntos de intersección, puede tardar unos segundos. Observa la diferencia entre el valor de la integral de la diferencia.. Por ejemplo, supongamos que queremos determinar el área de la región limitada por las gráficas de las funciones f (x) = x^2 y g (x) = 2x - 1, en el intervalo [0, 2]. Primero, debemos encontrar los puntos de intersección: x^2 = 2x - 1. x^2 - 2x + 1 = 0. (x - 1)^2 = 0. x = 1. Esto nos indica que las funciones se intersectan en x = 1.